Recall that if functions f(x) and g(x) are inverses, their compositions will equal x.
QUESTION A
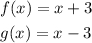
The compositions are calculated as follows:
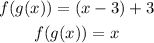
and
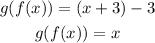
Therefore, f and g are inverses of each other.
QUESTION B
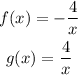
The compositions are calculated as follows:
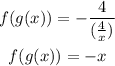
and
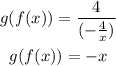
Therefore, f and g are not inverses of each other.