Question

O GRAPHS AND FUNCTIONSDetermining whether two functions are inverses of each other

Answer 1

Recall that if functions f(x) and g(x) are inverses, their compositions will equal x.

QUESTION A

`\begin{gathered} f(x)=x+3 \\ g(x)=x-3 \end{gathered}`

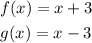
The compositions are calculated as follows:

`\begin{gathered} f(g(x))=(x-3)+3 \\ f(g(x))=x \end{gathered}`

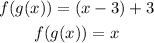
and

`\begin{gathered} g(f(x))=(x+3)-3 \\ g(f(x))=x \end{gathered}`

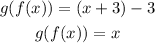
Therefore, f and g are inverses of each other.

QUESTION B

`\begin{gathered} f(x)=-(4)/(x) \\ g(x)=(4)/(x) \end{gathered}`

The compositions are calculated as follows:

`\begin{gathered} f(g(x))=-(4)/(((4)/(x))) \\ f(g(x))=-x \end{gathered}`

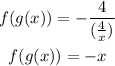
and

`\begin{gathered} g(f(x))=(4)/((-(4)/(x))) \\ g(f(x))=-x \end{gathered}`

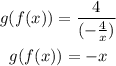
Therefore, f and g are not inverses of each other.