Question

How would I solve 16x^4-41x^2+25=0 ???

Answer 1

16x⁴ - 41x² + 25 = 0
16x⁴ - 16x² - 25x² + 25 = 0
16x²(x²) - 16x²(1) - 25(x²) + 25(1) = 0
16(x² - 1) - 25(x² - 1) = 0
(16x² - 25)(x² - 1) = 0
(16x² + 20x - 20x - 25)(x² - x + x - 1) = 0
(4x(4x) + 4x(5) - 5(4x) - 5(5))(x(x) - x(1) + 1(x) - 1(1)) = 0
(4x(4x + 5) - 5(4x + 5))(x(x - 1) + 1(x - 1)) = 0
(4x - 5)(4x + 5)(x + 1)(x - 1) = 0
4x - 5 = 0 or 4x + 5 = 0 or x + 1 = 0 or x - 1 = 0
+ 5 + 5 - 5 - 5 - 1 - 1 + 1 + 1
4x = 5 4x = -5 x = -1 x = 1
4 4 4 4
x = 1¹/₄ x = -1¹/₄

The solution set is equal to {(1¹/₄, -1¹/₄, -1, 1)}.

Answer 2

`16{ x }^( 4 )-41{ x }^( 2 )+25=0`


`{ x }^( 4 )={ ({ x }^( 2 )) }^( 2 )\\ \\ 16{ ({ x }^( 2 )) }^( 2 )-41{ x }^( 2 )+25=0`



First of all to make our equation simpler, we'll equal
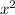
`x^(2)` to a variable like 'a'.

So,


`{ x }^( 2 )=a`

Now let's plug
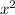
`x^(2)` 's value (a) into the equation.


`16{ ({ x }^( 2 )) }^( 2 )-41{ x }^( 2 )+25=0\\ \\ { x }^( 2 )=a\\ \\ 16{ (a) }^( 2 )-41{ a }+25=0`

Now we turned our equation into a quadratic equation.

(The variable 'a' will have a solution set of two solutions, but 'x' , which is the variable of our first equation will have a solution set of four solutions since it is a quartic equation (fourth-degree equation) )

Let's solve for a.

The formula used to solve quadratic equations ;


`\frac { -b\pm \sqrt { { b }^( 2 )-4\cdot t\cdot c } }{ 2\cdot t }`

The formula is used in an equation formed like this :


`t{ x }^( 2 )+bx+c=0`

In our equation,

t=16 , b=-41 and c=25

Let's plug the values in the formula to solve.


`t=16\quad b=-41\quad c=25\\ \\ \frac { -(-41)\pm \sqrt { -(41)^( 2 )-4\cdot 16\cdot 25 } }{ 2\cdot 16 } \\ \\ \frac { 41\pm \sqrt { 1681-1600 } }{ 32 } \\ \\ \frac { 41\pm \sqrt { 81 } }{ 32 } \\ \\ \frac { 41\pm 9 }{ 32 }`

So the solution set :


`\frac { 41+9 }{ 32 } =\frac { 50 }{ 32 } \\ \\ \frac { 41-9 }{ 32 } =\frac { 32 }{ 32 } =1\\ \\ a\quad =\quad \left\{ \frac { 50 }{ 32 } ,\quad 1 \right\}`

We found a's value.

Remember,


`{ x }^( 2 )=a`

So after we found a's solution set, that means.


`{ x }^( 2 )=\frac { 50 }{ 32 }`

and


`{ x }^( 2 )=1`

We'll also solve this equations to find x's solution set :)


`{ x }^( 2 )=\frac { 50 }{ 32 } \\ \\ \frac { 50 }{ 32 } =\frac { 25 }{ 16 } \\ \\ { x }^( 2 )=\frac { 25 }{ 16 } \\ \\ \sqrt { { x }^( 2 ) } =\sqrt { \frac { 25 }{ 16 } } \\ \\ x=\quad \pm \frac { 5 }{ 4 }`


`{ x }^( 2 )=1\\ \\ \sqrt { { x }^( 2 ) } =\sqrt { 1 } \\ \\ x=\quad \pm 1`

So the values x has are :


`\frac { 5 }{ 4 }` ,
`-\frac { 5 }{ 4 }` ,
`1` and
`-1`

Solution set :


`x=\quad \left\{ \frac { 5 }{ 4 } \quad ,\quad -\frac { 5 }{ 4 } \quad ,\quad 1\quad ,\quad -1 \right\}`

I hope this was clear enough. If not please ask :)