Given: A 90-foot rope from the top of a tree house to the ground forms a 45° angle of elevation from the ground.
Required: To determine the height of the tree house.
Explanation: The given problem can be represented as follows-
In the figure, AC represents the rope, and AB is the tree house. We need to determine the length of AB.
Recall the trigonometric ratio-
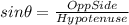
Thus, for triangle ABC we have-
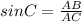
Substituting the values and solving for AB as-
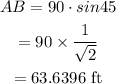
Thus,
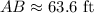
Final Answer: The top of the tree house is 63.6 ft high.