Question

A 3.4 kg mass weighs 33.32 N on the surfaceof a planet similar to Earth. The radius ofthis planet is roughly 6.4 × 106 m.Calculate the mass of of this planet. Thevalue of the universal gravitational constantis 6.67259 × 10−11 N · m2/kg2.Answer in units of kg.

Answer 1

We are given that a body of 3.4 kg has a weight of 33.32 N. We are asked to determine the mass of the planet. To do this we will use the following formula for the gravitational force between two masses:

`F_G=G(m_1m_2)/(r^2)`

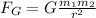
Where:

`\begin{gathered} F_G=\text{ gravitational force} \\ G=\text{ gravitational constant} \\ m_(1,)m_2=\text{ masses} \\ r=\text{ distance betwe}en\text{ the masses} \end{gathered}`

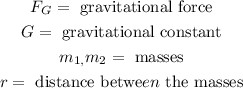
The gravitational force is equivalent to the weight is the object since this is the force that gravitation exerts on both masses. The distance between the masses is equivalent to the radius of the planet since the object is on the surface. Now we will solve for the mass 2 first by dividing both sides by the gravitational constant:

`(F_G)/(G)=(m_1m_2)/(r^2)`

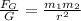
Now we multiply both sides by the square of "r":

`(F_Gr^2)/(G)=m_1m_2`

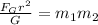
Now we divide both sides by the second mass:

`(F_Gr^2)/(m_2G)=m_1`

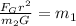
Now we substitute the values:

`((33.2N)(6.4*10^6m)^2)/((3.4kg)(6.67259*10^(-11)Nm^2))=m_1`

Now we solve the operations:

Therefore, the mass of the planet is 5.29 x 10^24 kilograms.