Answer:

Explanation:
we know that
If two lines are perpendicular
then
the product of their slopes is equal to minus one
so
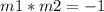
In this problem line AB and line PQ are perpendicular
Step 1
Find the slope of the line AB
The equation of the line AB is

isolate the variable y
 ------>
------>

The slope of the line AB is equal to
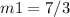
Step 2
Find the slope of the line PQ
remember that
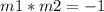
we have
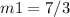 ----> slope line AB
----> slope line AB
so
substitute and solve for m2


Step 3
Find the equation of the line PQ
The equation of the line into point-slope form is equal to
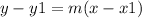
we have


substitute


 -----> multiply by
-----> multiply by
 both sides
both sides

 -----> divide by
-----> divide by
 both sides
both sides
 -----> multiply by
-----> multiply by
 both sides
both sides
