Question

Each edge of the winding walkway in the diagram is made of two circular arcs with a radius of 25 feet. The radius is depicted by a dashed line. If the width of the walkway is 5 feet, what is the difference of the lengths of the two edges of the walkway?

Answer choices:
0.50 feet
1.25 feet
1.80 feet
2.15 feet

View the attachment for the picture.

Answer 1

To find the length of any arc:
Find out what fraction of 360°, or in this case, 2π radians, the angle is.
Multiply that by the circumfrence of the circle. (2πr, of course)

The left side of the walkway can be found with


`(1.57)/(2\pi)*2\pi25\ +\ (1.32)/(2\pi)*2\pi30 = 78.85`

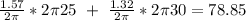
The right side of the walkway can be found with


`(1.57)/(2\pi)*2\pi30\ +\ (1.32)/(2\pi)*2\pi25 = 80.1`

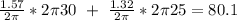
The difference between 80.1 and 78.85 is 1.25 ft.