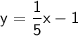Slope-intercept form is

, where
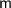
is the slope and

is the y-intercept.
Slope = -3, y-intercept = -1Plug in what we know:

 Slope = -2, y-intercept = -4
Slope = -2, y-intercept = -4Plug in what we know:

 Through: (-3,2) , slope=-1/3
Through: (-3,2) , slope=-1/3
Okay, here we use point-slope form, and the simplify to get it in slope-intercept form.
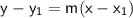
Where
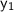
is the y-value of the point,
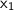
is the x-value of the point, and
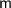
is the slope.
Plug in what we know:
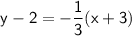
Distribute -1/3 into the parenthesis:

Add 2 to both sides:
 Through: (3,2) and (0,-5)
Through: (3,2) and (0,-5)
Now we plug this into the slope-formula to find the slope, plug the slope and one of these points into point-slope form, then simplify to get it in slope-intercept form.

(3, 2), (0, -5)
x1 y1 x2 y2
Plug in what we know:
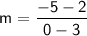
Subtract:
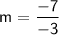
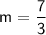
Plug this into point-slope form along with any point.
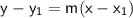
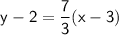
Distribute 7/3 into the parenthesis:
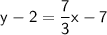
Add 2 to both sides:
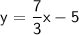
x-5y-5=0
Add 5 to both sides:
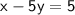
Subtract 'x' to both sides:
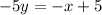
Divide -5 to both sides: