Question

Graph the function with the given domain then identify the range of the function

Y=3x-2 domain (greater than or equal to sign) 0

Answer 1

When the domain is ≥ to 0, that basically means that x must be ≥ 0.
Imagine what that looks like.
It would just be the right side of the coordinate plane, right? Because the left side would have negative x values.

We're basically just going to be graphing the line
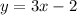
`y=3x-2`, except only the part on the right side of the coordinate plane because of course x ≥ 0.

When you have an equation in the form of
`y=mx+b`,
`b` is going to be the y-intercept (the point where the line intersects the y-axis) and
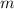
`m` is going to be the slope.

Since the y-intercept is -2, draw a point at (0, -2).

Then, use the slope to find another point on the line.
The slope is 3, which as a fraction would be
`\frac{3}1`.
Slope = rise over run, so basically every change of 1 in x = a change of 3 in y.
Draw a point 3 up and 1 over from (0, -2). (at (1, 1))

Then draw a line through the two points we have graphed. Don't draw past the y-axis on the left side, because of course x ≥ 0.

And there you go!

The range of the function is basically the possible values y can have.
Well, since it's not going any lower than the y-intercept (0, -2), the range is ≥ -2.