Question

HELP PLEASE I WILL GIVE BEST ANSWER

Angela is studying two types of birds. She measures the wingspan, in inches, of five Type 1 birds and five Type 2 birds.

What can she infer about the wingspans of the two types of birds?

Type 1: {18, 24, 20, 22, 26}
Type 2: {24, 21, 19, 26, 30}

A.
Type 1 and Type 2 birds have similar wingspan distributions.

B.
Type 1 and Type 2 birds have somewhat similar wingspan distributions.

C.
Type 1 birds and Type 2 birds do not have similar wingspan distributions.

D.
Type 1 birds and Type 2 birds have identical wingspan distributions.

Answer 1

Type 1 and Type 2 birds have similar wingspan distributions.

Explanation:

Answer 2

Explanation:

The given data set for type 1 of birds is:

Type 1: {18, 24, 20, 22, 26}

Type 2: {24, 21, 19, 26, 30}

Mean of the type 1 data is:

`Mean=(18+24+20+22+26)/(5)=(110)/(5)=22`

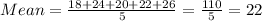
Data
`(x-{\overline{x})^2`

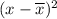
18 16

24 4

20 4

22 0

26 16

Now, mean average of squares is:

`m=(40)/(5)=8`

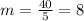
Standard deviation=
`SD=√(8)=2.828`

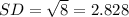
Now, the difference of mean and its standard deviation of type 1 data set is:

=22-2.828

Difference =19.172

The given data set for type 2 of birds is:

Type 2: {24, 21, 19, 26, 30}

Mean of the type 2 data is:

`Mean=(24+21+19+26+30)/(5)=(120)/(5)=24`

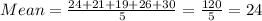
Data
`(x-{\overline{x})^2`

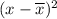
24 0

21 9

19 25

26 4

30 36

Now, mean average of squares is:

`m=(74)/(5)`

`m=14.8`

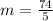
Standard deviation=
`SD=√(14.8)=3.84`

Now, the difference of mean and its standard deviation of type 2 data set is:

=24-3.84

Difference=20.16

Since, the difference of mean and standard deviation of both type 1 and type 2 data set is different, therefore, Type 1 birds and Type 2 birds do not have similar wingspan distributions.

Hence, option C is correct.