Question

Find an equation of the line satisfying the given conditions

Through (6,4); perpendicular to 3X + 5Y =38

Answer 1

`(6,4); 3x + 5y =38 \ subtract \ 3x \ from \ each \ side \\ \\ 5y = -3x + 8 \ divide \ each \term \ by \ 5 \\ \\ y = -\frac{3} {5}x + (38)/(5)\\ \\ The \ slope \ is :m _(1) = - (3)/(5) \\ \\ If \ m_(1) \ and \ m _(2) \ are \ the \ gradients \ of \ two \ perpendicular \\ \\ lines \ we \ have \ m _(1)*m _(2) = -1`


`m _(1) \cdot m _(2) = -1 \\ \\ -(3)/(5) \cdot m_(2)=-1 \ \ / \cdot (-(5)/(3)) \\ \\ m_(2)=(5)/(3)`


`Now \ your \ equation \ of \ line \ passing \ through \ (6,4) would \ be: \\ \\ y=m_(2)x+b \\ \\4=(5)/(\\ot3^1) \cdot \\ot 6^2 + b`


`4=5 \cdot 2+b\\ \\4=10+b \\ \\b=4-10\\ \\b=-6 \\ \\ y = (5)/(3)x -6`

Answer 2

To answer this, we will need to know:

• The slope of the equation we are trying to get
• The point it passes through using the

First, we will need to find the slope of this equation. To find this, we must simplify the equation
`3x+5y=38` into
`y=mx+b` form. Lets do it!


`3x+5y=38`
=
`5y = -3x+38` (Subtract 3x from both sides)
=
`y= -(3)/(5)x+ (38)/(5)` (Divide both sides by 5)

The slope of a line perpendicular would have to multiply with the equation we just changed to equal -1. In other words, it would have to equal the negative reciprocal.

The negative reciprocal of the line given is
`(5)/(3)`.

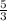
Now that we know the slope, we have to find out the rest of the equation using the slope formula, which is:


`(y-y _(1) )/(x- x_(1) )=m`

Substituting values, we find that:


`(y-4)/(x-6)= (5)/(3)`

By simplifying this equation to slope-intercept form (By cross-multiplying then simplifying), we then get that:


`y= (5)/(3)x-6` , which is our final answer.

Thank you, and I wish you luck.