Question

Solve 2x^2+8x-7=-2 by completing the square

Answer 1

2x² + 8x - 7 = -2
+ 2 + 2
2x² + 8x - 5 = 0
x = -(8) +/- √((8)² - 4(2)(-5))
2(2)
x = -8 +/- √(64 + 40)
4
x = -8 +/- √(104)
4
x = -8 +/- 2√(26)
4
x = -2 + 0.5√(26)
x = -2 + 0.5√(26) x = -2 - 0.5√(26)

Answer 2

How to complete the square:

Step 1: Get all constants on one side.


`2x^2+8x-7=-2\\2x^2+8x=5`

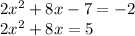
Step 2: If x² has a coefficient, divide it out.


`2x^2+8x=5 \\ x^2+4x=\frac2{1}2`

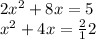Step 3: Halve the coefficient of x, square it, and add it to both sides.
(In this case, half of 4 is 2, and 2² is 4, so we add 4 to both sides.


`x^2+4x=\frac{5}2\\x^2+4x+2=6\frac{1}2`

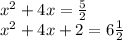Step 4: Factor the left side. (And if the right side is a mixed number, change it to an improper fraction to make step 5 easier)
We set it up so that it will be a perfect square trinomial, so it'll always be equal to (x+half the coefficient of x)².


`x^2+4x+2=6\frac{1}2\\(x+2)^2=\frac{13}2`

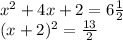
Step 5: Take the square root of each side.

(x+2)^2=\frac{13}2\\\sqrt{(x+2)^2}=\sqrt{\frac{13}2}

Step 6: Simplify and solve for x.


`√((x+2)^2)=\sqrt{\frac{13}2} \\ x+2=(√(13))/(√(2)) = \frac{√(26)}2 \\\\ \boxed{x = -2\±\frac{√(26)}2}`

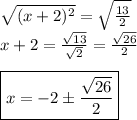
(Decimal answers if needed: approx -4.5495 and 0.54951)