Question

What is the amplitude, period, and phase shift of f(x) = -4 sin(2x + π) - 5?

Answer 1

f(x) = -4sin(2x + π) - 5

Amplitude
A = -π

Period
2π = 2π = π
B 2

Phase Shift
-C = -π = ≈ 1.57
B 2

Answer 2

Amplitude of the function is 4, period of the function is π and phase shift of the function is
`-(\pi)/(2)`.

Explanation:

The given function is

`f(x)=-4\sin(2x+\pi)-5` .... (1)

The general form of a sine function is

`f(x)=A\sin(Bx+C)+D` .... (2)

where, |A| is amplitude,
`(2\pi)/(B)` is period,
`-(C)/(B)` is phase shift and D is midline.

From (1) and (2) we get

`A=-4,B=2, C=\pi,D=-5`

`|A|=|-4|=4`

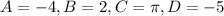
Amplitude of the function is 4.

`(2\pi)/(B)=(2\pi)/(2)=\pi`

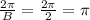
Period of the function is π.

`-(C)/(B)=-(\pi)/(2)`

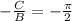
Therefore the phase shift of the function is
`-(\pi)/(2)`.