The triangle ABC is an isosceles with AB=AC.
BC=48
Now given that
DE:DF=5:7.
Since DE is perpendicular to AB and DF is perpendicular to AC, therefore,
BD:DC=5:7
It happens because as DE:DF=5:7, the ratio of the area of the two reight angle triangles is also 5:7.
So, their base must be in the same ration.
Now, two sides are in same ratio, by default, their third sides i.e., BD and DC have the ratio 5:
Since, BC=48, therefore,
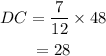
Hence, the correct option is (D).