Question

`{25x}^(2) - 4x + 16`is NOT a perfect square trinomial. Which criteria are not met?

Answer 1

b is not the product of 2 times the product of the roots because:

Step-by-step explanation:

The initial expression is:

25x² - 4x + 16

It is a trinomial because it has three terms: 25x², - 4x, and 16.

Additionally, the 1st and 3rd term are perfect squares because:

`\begin{gathered} \sqrt[]{25x^2}=5x^{} \\ \sqrt[]{16}=4 \end{gathered}`

Finally, the only correct statement is that b is not the product of 2 times the product of the roots because:

`\begin{gathered} -4x\\e2(5x)(4) \\ -4x\\e40x \end{gathered}`

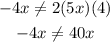
Therefore, the answer is: b is not the product of 2 times the product of the roots because: