Question

Find the measure of interior angle C of hexagon OCEANS in which the

measure of the interior angles are:
O: 3x + 15, C: 2x + 30, E: 5x + 10, A: 2x + 55, N: 2x + 60, and S: x - 35.

Answer 1

The measure of the interior angle C is
`108^(o)`.

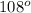Explanation:

Sum of angles in a polygon = (n - 2) x 180

where n is the number of sides of the polygon.

For a hexagon, n = 6. So that;

Sum of angles in a hexagon = (6 - 2) x 180

= 4 x 180

=
`720^(o)`

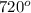
Sum of angles in a hexagon =
`720^(o)`

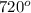
⇒ 3x + 15 + 2x + 30 + 5x + 10 + 2x + 55 + 2x + 60 + x - 35 =
`720^(o)`

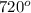
15x + 135 =
`720^(o)`

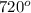
15x =
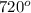`720^(o)` - 135

15x = 585

x =
`(585)/(15)`

=
`39^(o)`

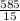
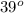
But,

C = 2x + 30

= 2(39) + 30

= 78 + 30

=
`108^(o)`

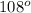
The measure of the interior angle C is
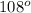`108^(o)`.