Question

Tree is casting a 35 ft shadow when the sun is at a 56° angle of elevation. How tall is the tree?

Answer 1

Given:

There are given that the 35 ft shadow when the sun is at 56 degrees.

Step-by-step explanation:

To find the tall of the tree, first we need to draw the image:

So,

The image of the given statement is:

Now,

from the given image, we need to find the value of the length of the tree.

So,

To find the length of the tree, we need to use the tan function:

Then,

From the formula of tan function:

`tan56^(\circ)=(AB)/(BC)`

Then,

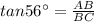
Then,

`\begin{gathered} tree=tan56^(\circ)*35 \\ tree=51.89 \end{gathered}`

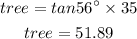
Final answer:

Hence, the height of the tree is 52 ft.