We will have the following:
We have that for each "piece" of a piecewise function we have parameters that describe the function at intervals or points. To calculate the limit of such a function we must use the same parameters to analyze the function at the points delimited by them, and to completly determine the nature of the limit of each point you apply the lateral limits under those parameters.
***Example***
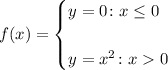
Now, we want to find the limit when x approaches 0, that is:
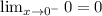
and:
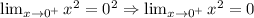
So, the limit when the piecewise function appoaches 0 is 0. [Even under lateral limits]
Here's the graph: