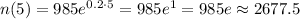Question

The number of bacteria in a culture is given by the function n(t)=985e^.2twhere t is measured in hours.(a) What is the relative rate of growth of this bacterium population?(b) What is the initial population of the culture (at t=0)(c) How many bacteria will the culture contain at time t=5

Answer 1

(a) The relative rate of growth is 0.2

(b) The initial population is 985

(c) The amount of bacteria at time t = 5 is 2677.5

Step-by-step explanation:

An exponential equation to model exponential growth is:

`G(t)=Ie^(rt)`

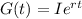
Where:

• I is the initial population

,

• r is the rate of relative growth

,

• t is the time

We have in this problem:

`n(t)=985e^(0.2t)`

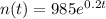
Then:

(a) The relative rate is 0.2

(b) The initial population is 985

(c) To find the population at t = 5, we evaluate the equation:

`n(5)=985e^(0.2\cdot5)=985e^1=985e\approx2677.5`