Question

On what intervals is the graph of f(x)=x^3-2x^2+5x+1 increasing?

On what intervals is the graph of f(x)=0.5x^2-6 decreasing?

On what intervals is the graph of f(x)=
`(x+1)/(x-1)` increasing?

Answer 1

`f(x)=x^3-2x^2+5x+1\\ f'(x)=3x^2-4x+5\\ 3x^2-4x+5=0\\\Delta=(-4)^2-4\cdot3\cdot5=16-60=-44`

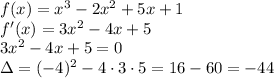
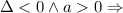
`\Delta<0 \wedge a>0 \Rightarrow` the graph of the parabola is above the x-axis, so the derivative is always positive and therefore the initial function is increasing in its whole domain.


`f(x)=0.5x^2-6\\ f'(x)=x`
The function is decreasing when its first derivative is negative. The first derivative of this function is negative for
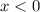
`x<0` so for
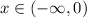
`x\in(-\infty,0)` the function is decreasing.


`f(x)=(x+1)/(x-1)\qquad(x\\ot=1)\\ f'(x)=(x-1-(x+1))/((x-1)^2)=-(2)/((x-1)^2)`
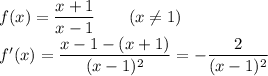
The function is increasing when its first derivative is positive. The first derivative of this function is always negative therefore this function is never increasing.