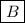Question

Help PleAsE??

What is the point-slope form of the equation of a line that passes through the point (6, −8) and has a slope of −2?
A.y+8=2(x-6)

B.y+8=-2(x-6)

C.y-6=-2(x-8)

D.y-8=-2(x+6)

Answer 1

Point slope form is:

`\sf {y - y_1 = m(x - x_1)}`

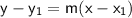
Where
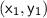
`\sf{(x_1,y_1)}` is the point and
`\sf{m}` is the slope.

So from your question:


`\sf{ x_1 = 6}`

`\sf{y_1 = -8}`

`\sf{m = -2}`

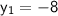
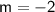
Plug them into the equation for point slope form:


`\sf {y - y_1 = m(x - x_1)}`

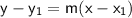
Becomes when you plug it in:


`\sf{y-(-8) = -2(x - 6)}`

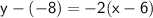
And when you subtract a negative that becomes addition so:


`\sf{y+ 8 = -2(x - 6)}`

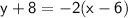
And that would correlate to answer choice
`\sf{\boxed{B}}`

Answer 2

y - y1 = m(x - x1)

Where 'y1' is the y-value of the point, 'x1' is the x-value of the point, and 'm' is the slope.

So in this case:

y1 = -8
x1 = 6
m = -2

Plug them in:

y - (-8) = -2(x - 6)

or

y + 8 = -2(x - 6)