Question

The annual birth rate for a population of a given country is represented by the function y= 918397(0.9763)^t where “t” represents the Number of years since 2018.

5a.) Identify the number of annual births in this country in 2018.

5b.) Identify the percent decrease in birth rates given in the function.

5c.) Using the given model, identify the expected Number of births in 2021 (4 years after 2018)

Answer 1

The initial number of annual births in 2018 is 918,397

The percent decrease in birth rates is 2.37%

The expected number of births in 2021 is 834,379

Explanation:

Exponential Decay Function

The exponential function is frequently used to model natural decaying processes, where the change is proportional to the actual quantity.

An exponential decaying function is expressed as:

`C(t)=C_o\cdot(1-r)^t`

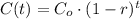
Where:

C(t) is the actual value of the function at time t

Co is the initial value of C at t=0

r is the decaying rate, expressed in decimal

We are given the function that models the annual birth rate for a population of a given country:

`y= 918,397(0.9763)^t`

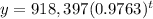
Where t represents the number of years since 2018.

a.) We can identify the variables with the actual model by comparing with the general equation, thus: Co=918,397 and 1-r=0.9763.

Solving for r we have r=1-0.9763=0.0237.

This means the initial number of annual births in 2018 (t=0) is 918,397

b.) The percent decrease in birth rates is r=0.0237 = 2.37%

c.) To find the expected number of births in 2021 (t=4 years), we substitute the value of t in the equation of the model:

`y= 918,397(0.9763)^4`

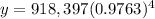
Calculating:

y = 834,379

The expected number of births in 2021 is 834,379