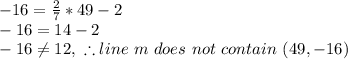The equation of a line is usually written in what's called
slope-intercept form.
Slope-intercept form is written as y = mx + b where m = slope and b = the y-intercept.
The slope of a line can easily be found just by using two points on the line. The slope is equal to the rise over the run, or the difference in y over the difference in x, between the two points.
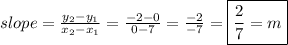
The y-intercept of the line is the point at which it intersects the y-axis. (The vertical axis.) All points on the y-axis have an x coordinate of 0, so we would then add or subtract the rise and run to a point on the line until we reached x = 0.
Fortunately, we already have this point! It's (0, -2)!
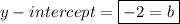
Now we just need to put our slope and y-intercept into the equation.
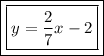
And to test if a point is on this line, just plug in the x and y coordinates and see if the equation is true!