Question

A survey of a group of seventh graders and a group of teachers at a local middle school asked how many siblings they each have. The dot plots below show the results.

Students
A dot plot titled Students. A number line going from 0 to 9 labeled number of siblings. There are 2 dots above 0, 4 above 1, 7 above 2, 5 above 3, 2 above 4, and 0 above 5, 6, 7, 8, and 9.

Teachers
A dot plot titled Teachers. A number line going from 0 to 9 labeled Number of siblings. There is 1 dot above 0, 3 dots above 1, 2 above 2, 4 above 3, 5 above 4, 3 above 5, 1 above 6, 0 above 7, 1 above 8, and 0 above 9.

Which compares the modes of the data?

Answer 1

To obtain the information requested in the question, the following steps are necessary:

Step 1: Write out the values from the box plot as a sequence of numbers, as follows:

`0,0,0,1,1,1,2,2,2,3,3,3,3,3,3,4,4,4,6`

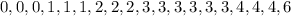
Step 2: Now, that we have the values written out as above, we can proceed to answering the questions, as follows:

a) To obtain the number of students that have at least 4 siblings (that is, more than 4 siblings), we count the number of times the numbers 4 and 6 occur.

By counting, we get: 5

Therefore, the number of students that have at least 4 siblings is: 5

b) To obtain the number of students that have no siblings (0 siblings), we count the number of times the number 0 occurs.

By counting, we get: 3

Therefore, the number of students that have at least 0 siblings is: 3

c) To obtain the mean (average) number of siblings, we proceed as follows:

`average=\frac{sum\text{ of all the number of siblings}}{\text{total number of students}}`

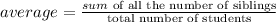
Therefore:

`\begin{gathered} \text{average}=(0+0+0+1+1+1+2+2+2+3+3+3+3+3+3+4+4+4+6)/(20) \\ \text{average}=(45)/(20)=(9)/(4)=2.25 \\ \text{average}=2.25 \end{gathered}`

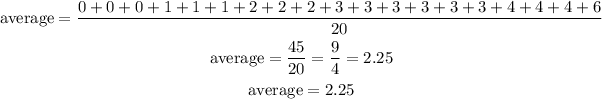
Therefore, the mean (average) number of siblings is 2.25 (approximately 2)