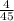Question

a bag has red, black and white stones. there are 2 red stones, twice as many black as red, and the remaining two-fifths of the stones are white. If 2 stones are removed WITHOUT replacement, what is the probability that the first stone is red and the second stone is white?2/45; 4/45; 2/11; 2/9 or 7/9

Answer 1

A bag has red, black and white stones.

There are 2 red stones.

Twice as many black as red, that means 4 black stones.

The remaining two-fifths of the stones are white.

That is,

If three-fifth of the stones are 6.

Then, two fifth of the stones are,

`\begin{gathered} (2)/(3)*6=2*2 \\ =4 \end{gathered}`

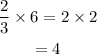
Therefore, there are 4 white stones.

The probability that the first stone is red and the second stone is white is,

Using the formula,

`^nC_r=(n!)/((n-r)!r!)`

Here, n is the total number of items and r is the number of selected items.

`\begin{gathered} (^2C_1)/(^(10)C_1)*(^4C_1)/(^9C_1)=((2!)/((2-1)!1!))/((10!)/((10-1)!1!))*((4!)/((4-1)!1!))/((9!)/((9-1)!1!))\Rightarrow((2*1)/(1))/((10*9!)/(9!))*((4*3!)/(3!))/((9*8!)/(8!)) \\ =(2)/(10)*(4)/(9) \\ =(1)/(5)*(4)/(9) \\ =(4)/(45) \end{gathered}`

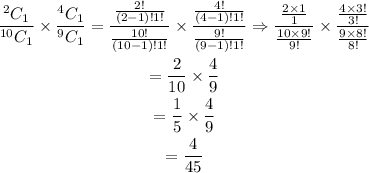
Hence, the correct option is B.

The probability that the first stone is red and the second stone is white is,

`(4)/(45)`