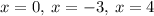Question

Consider the function f (x) = x (x+3)(x – 4).
What are the zeros of the function?

Answer 1

The solutions are:

`x=0,\:x=-3,\:x=4`

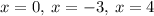
Explanation:

Given the function

`f(x) = x(x+3)(x - 4)`

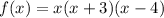
In order to determine the zeros of the function, we substitute f(x) = 0

`0\:=\:x\left(x+3\right)\left(x\:-\:4\right)`

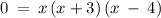
switch sides

`x\left(x+3\right)\left(x-4\right)=0`

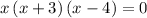
Using the zero factor principle

if ab=0, then a=0 or b=0 (or both a=0 and b=0)

`x=0\quad \mathrm{or}\quad \:x+3=0\quad \mathrm{or}\quad \:x-4=0`

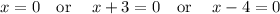
Thus,

x = 0

and solving x + 3 = 0

x + 3 = 0

subtracting 3 from both sides

x + 3 - 3 = 0 - 3

x = -3

and solving x - 4 = 0

x - 4 = 0

x - 4 + 4 = 0 + 4

x = 4

Therefore, the solutions are:

`x=0,\:x=-3,\:x=4`