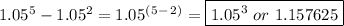Question

a mouse population starts with 2,000 mice and grows at a rate of 5% per year. The number of mice after t years can be modeled by the equation, P(t)=2000(1.05)^t. What is the average rate of change in the number of mice between the second year and the fifth year, rounded to the nearest whole number

Answer 1

Let's disect our equation.


`P_t = 2000*1.05^t`

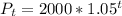
The 2000 is the initial number. Each year, there is 5% more. Add that to the 100% already there and you get 105%, in decimal form 1.05. Each year that is multiplied onto 2000, so we represent it as an exponent ^t. The 1.05^t is our rate of change.

Now let's try for 2 and 5.

`P_2 = 2000*1.05^2`

`P_5 = 2000*1.05^5`

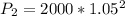
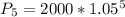
The rate of change would be the difference between the two.


`1.05^5 - 1.05^2 = 1.05^(^5^-^2^) = \boxed{1.05^3\ or\ 1.157625}`