Question

Write a system of equations to describe the situation below, solve using any method, and fill in the blanks. Olivia and her sister Emily are making baby blankets to sell at a boutique. Olivia has already completed 6 blankets and can finish 5 more blankets per day. Emily has already completed 9 blankets and can finish 2 more blankets per day. At some point, they will have completed the same number of blankets. How many blankets will each woman have made? How long will that take?

Answer 1

Let:

yo = Number of blankets per day for Olivia

ye = Number of blankets per day for Emily

x = number of days

so:

`\begin{gathered} yo(x)=6+5x \\ ye(x)=9+2x \end{gathered}`

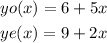
At some point, they will have completed the same number of blankets, so:

`\begin{gathered} yo(x)=ye(x) \\ 6+5x=9+2x \\ solve_{\text{ }}for_{\text{ }}x\colon \\ 5x-2x=9-6 \\ 3x=3 \\ x=1 \end{gathered}`

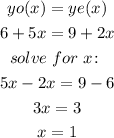
for Olivia:

`\begin{gathered} ye(1)=6+5(1)=11 \\ yo(1)=9+2(1)=11 \end{gathered}`

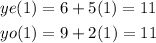
they will make 11 blankets and it will take one day.