Question

Ray's pizza serves small and large pizzas. A small pizza has a diameter of 10 inches and is sliced into six equal slices. A large pizza has a diameter of 18 inches and is sliced into twelve equal slices. If Charles ate five slices of large pizza and Julie ate seven slices of small pizza, who ate the most pizza in terms of area?

Answer 1

Step-by-step explanation

To solve this problem, we consider the area of a circular region with angle θ and radius r:

`A(r,\theta)=\pi r^2*(\theta)/(360\degree).`

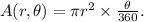
From the statement, we know that we have two pizzas:

1) The small pizza has:

• a diameter and a radius:

`d_s=10\text{ in}\rightarrow r_s=(d_s)/(2)=\frac{10\text{ in}}{2}=5\text{ in,}`

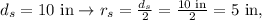
• each of the six equal slices has an angle:

`φ_s=(360\degree)/(6)=60\degree.`

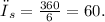
2) The large pizza has:

• a diameter and a radius:

`d_l=18\text{ in}\rightarrow r_l=(d_l)/(2)=\frac{18\text{ in}}{2}=9\text{ in,}`

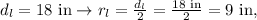
• each of the two equal slices has an angle:

`φ_l=(360\degree)/(12)=30\degree.`

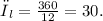
(1) If Charles ate 5 slices of the large pizza, he ate an angle θ = 5*φl = 5*30° = 150°. Using the formula from above, we find that the area eaten by Charles is:

`A(r_l=9\text{ in},\theta=150\degree)=\pi(9\text{ in})^2\cdot(150\degree)/(360\degree)\cong106.03\text{ in}^2.`

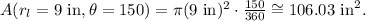
(2) If Julie ate 7 slices of the big pizza, she ate an angle θ = 7*φs = 7*60° = 420°. Using the formula from above, we find that the area eaten by Charles is:

`A(r_s=5\text{ in},\theta=420\degree)=\pi(5\text{ in})^2\cdot(420\degree)/(360\degree)\cong91.63\text{ in}^2.`

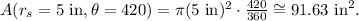
We have found that Charles ate an area of 106.03 in² and Julie an area of 91.63 in². We conclude that Charles ate more pizza than Julie.

Answer

Charles ate most pizza in terms of area.