Question

Please help me. The grade you make on your exam varies directly with the number of correct answers you get on the exam. Answering 32 questions correctly will give you a grue of 80. What is the constant of variation? Write an equation to represent this situation. y= How many questions do you need to answer correctly to get a grade of 90?

Answer 1

a) k = 2.5

b) y = 2.5x

c) the number of questions you need to answer correctly to get a grade of 90 is 36 correct answers.

Step-by-step explanation:

The grade you make on your exam varies directly with the number of correct answers you get on the exam.

Let y represent the grades you make

Let x represent the number of correct answers you get on the exam

y is directly proportional to x:

y ∝ x

where ∝ represent the direct proportion

To remove the ∝ (the proportion symbol), we will equate both variables and add a constant.

`\begin{gathered} \text{y = kx} \\ \text{where k = constant of proportionality} \end{gathered}`

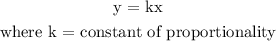
Answering 32 questions correctly will give you a grade of 80:

when x = 32, y =80

Let's find the value of k

`\begin{gathered} 80\text{ = k}*32 \\ k\text{ = }(80)/(32) \\ k=\text{ 2.5} \end{gathered}`

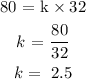
Hence, the constant of the variation = k = 2.5

An equation that represents this situation is the relationship between y and x.

To get the relationship between y and x, we will insert the value of k in the formula above:

y = kx

y = 2.5x

Therefore, an equation that represents this situationis y = 2.5x

When grade = 90, number of correct answers is unknown:

y = 90, x = ?

We will use the equation that represent the situation to find x

y = 2.5x:

90 = 2.5x

x = 90/2.5

x = 36

Therefore, the number of questions you need to answer correctly to get a grade of 90 is 36 correct answers.