Question

Jerome went apple picking with his family. In his bag he had 4 Granny Smith apples, 2 Honeycrisp apples, 3 Gala apples, and 1 Fuji apple. What is the probability that he will pick a Granny Smith apple out of his bag, replace it, and then choose a Honeycrisp apple? as a simplified fraction.

Answer 1

The information given states the following;

`\begin{gathered} \text{Granny Smith}=4 \\ \text{Honey Crisp}=2 \\ \text{Gala}=3 \\ \text{Fuji}=1 \\ \text{Total}=10 \end{gathered}`

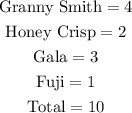
The total number of apples is 10.

Hence, for the experiments, we would have;

`\begin{gathered} P\lbrack E\rbrack=\frac{Number\text{ of required outcomes}}{Number\text{ of all possible outcomes}} \\ P\lbrack\text{Granny Smith\rbrack}=(4)/(10) \\ P\lbrack\text{Granny SSmith\rbrack}=(2)/(5) \\ \text{Similarly, after replacing the apple he would have;} \\ P\lbrack\text{Honey Crisp\rbrack}=(2)/(10) \\ P\lbrack\text{Honey Crisp\rbrack}=(1)/(5) \\ \end{gathered}`

The probability that he would pick a Granny Smith apple, replace it, and then choose a Honey Crisp apple is calculated as follows;

`\begin{gathered} P=P\lbrack granny\text{ smith\rbrack x P\lbrack{}honey crisp\rbrack} \\ P=(2)/(5)*(1)/(5) \\ P=(2)/(25) \end{gathered}`

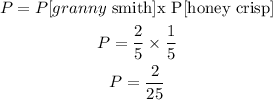
ANSWER:

The probability is therefore;

`(2)/(25)`