Question

For the function, f(x)=(9x+7)/(2x+4)

a. Find the critical points or explain, with a derivative, why there are no critical points.
b. Find the x and y coordinates of the absolute maximum and absolute minimum of f(x) in the interval [-10, 7]. Be sure to show all the necessary supporting calculus.
c. Find the x and y coordinates of the absolute maximum and absolute minimum of f(x) in the interval [0, 5]. Be sure to show all the necessary supporting calculus.

Answer 1

A.
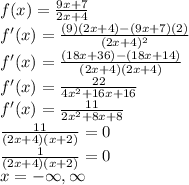
`f(x)=(9x+7)/(2x+4)\\f'(x)=((9)(2x+4)-(9x+7)(2))/((2x+4)^2)\\f'(x)=((18x+36)-(18x+14))/((2x+4)(2x+4))\\f'(x)=(22)/(4x^2+16x+16)\\f'(x)=(11)/(2x^2+8x+8)\\(11)/((2x+4)(x+2))=0\\(1)/((2x+4)(x+2))=0\\x=-\infty,\infty` - There are no critical points because the graph is neither continuous nor smooth. There is a discontinuity at x = 2.

B.
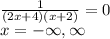
`(1)/((2x+4)(x+2))=0\\x=-\infty,\infty` - The absolute maximum is f(lim⇒-2_-) = infinity. The absolute minimum is f(lim⇒-2_+) = -infinity. This applies to the interval [-10, 7].

C.
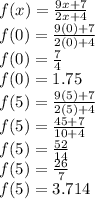
`f(x)=(9x+7)/(2x+4)\\f(0)=(9(0)+7)/(2(0)+4)\\f(0)=(7)/(4)\\f(0)=1.75\\f(5)=(9(5)+7)/(2(5)+4)\\f(5)=(45+7)/(10+4)\\f(5)=(52)/(14)\\f(5)=(26)/(7)\\f(5)=3.714` - The absolute maximum is f(5) = 26/7 or 3.714. The absolute mimimum is f(0) = 1.75. This applies to the interval [0, 5]. Proof: graph f(x) at [0, 5] on a graph or graphing calculator.