Question

Which binomial is a factor of 8x^2y^3-18y

Answer 1

Please check the explanation.

Explanation:

Given the expression

`8x^2y^3-18y`

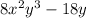
Apply exponent rule:
`a^(b+c)=a^ba^c`

`8x^2y^3-18y=8yy^2-18y` ∵
`x^2y^3=yy^2`

`=4\cdot \:2yy^2+9\cdot \:2y`

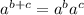
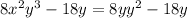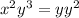
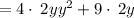
Factor out common term 2y

`=2y\left(4x^2y^2-9\right)`

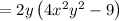
We know that the Binomial is an expression that consists of two terms. Thus,

(4x²y²- 9) represents the binomial factor of
`8x^2y^3-18y`

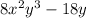
We can further simplify by Factoring 4x²y² - 9: (2xy + 3) (2xy - 3)

`=2y\left(2xy+3\right)\left(2xy-3\right)`

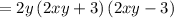
Here:

(2xy + 3) and (2xy -3) are the binomial factors of
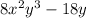`8x^2y^3-18y` as each of them consists of two terms.