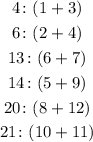Question

the numbers from 1 to 12 are written on separate papers folded and shaken. 6 students pick a pair each and adds the number..they sum of the pair of each student is 4,6,13,14,20,21.find the numbers in each pair

Answer 1

To answer this question, we will have to list the possible combinations for each outcome.

We can'rt have repetitions and we only have integer numbers from 1 to 12.

So, for 4, we would have the possible pairs of 1 and 3 or 2 and 2, but since we don't have repeating numbers, we only can have 1 and 3.

We will need to do this for every number:

`\begin{gathered} 4\colon(1+3) \\ 6\colon(1+5),(2+4) \\ 13\colon(1+12),(2+11),(3+10),(4+9),(5+8),(6+7) \\ 14\colon(2+12),(3+11),(4+10),(5+9),(6+8) \\ 20\colon(8+12),(9+11) \\ 21\colon(9+12),(10+11) \end{gathered}`

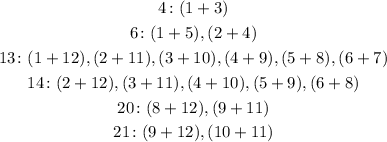
Now, the outcome of 4 has onle the possible pair of 1 and 3, so we already know that the first par is 1 and 3.

Since we can't have repetitions, every other pair that has either 1 or 3 can't happen, so:

`\begin{gathered} 4\colon(1+3) \\ 6\colon\cancel{\mleft(1+5\mright)},(2+4) \\ 13\colon\cancel{(1+12)},(2+11),\cancel{\mleft(3+10\mright)},(4+9),(5+8),(6+7) \\ 14\colon(2+12),\cancel{\mleft(3+11\mright)},(4+10),(5+9),(6+8) \\ 20\colon(8+12),(9+11) \\ 21\colon(9+12),(10+11) \end{gathered}`

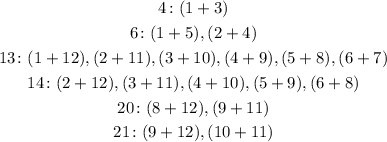
Now, the outcome of 6 has only one possible pair: 2 and 4. So, we need to exclude any other pair with either 2 or 4:

`\begin{gathered} 4\colon(1+3) \\ 6\colon(2+4) \\ 13\colon\cancel{(1+12)},\cancel{(2+11)},\cancel{\mleft(3+10\mright)},\cancel{\mleft(4+9\mright)},(5+8),(6+7) \\ 14\colon\cancel{\mleft(2+12\mright)},\cancel{\mleft(3+11\mright)},\cancel{\mleft(4+10\mright)},(5+9),(6+8) \\ 20\colon(8+12),(9+11) \\ 21\colon(9+12),(10+11) \end{gathered}`

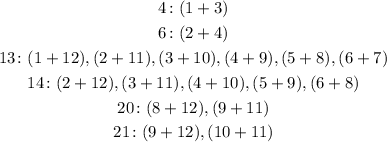
Now, notice that if we pick the pair 5 and 8 for the outcome 13, both remaining possbile outcomes for 14 would be impossible, because each has either 5 or 8. This means that the outcome 13 can't be 5 and 8, so it has to be 6 and 7, so we can exclue the other pairs with 6 or 7:

`\begin{gathered} 4\colon(1+3) \\ 6\colon(2+4) \\ 13\colon(6+7) \\ 14\colon\cancel{\mleft(2+12\mright)},\cancel{\mleft(3+11\mright)},\cancel{\mleft(4+10\mright)},(5+9),\cancel{\mleft(6+8\mright)} \\ 20\colon(8+12),(9+11) \\ 21\colon(9+12),(10+11) \end{gathered}`

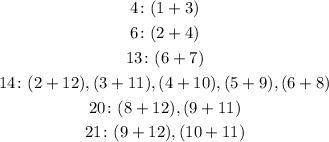
This makes the only possible pair for 14 to be 5 and 9, so we can exclude the other pairs with either 5 or 9:

`\begin{gathered} 4\colon(1+3) \\ 6\colon(2+4) \\ 13\colon(6+7) \\ 14\colon(5+9) \\ 20\colon(8+12),\cancel{\mleft(9+11\mright)} \\ 21\colon\cancel{\mleft(9+12\mright)},(10+11) \end{gathered}`

And this leave us with only one possible pair for 20 and 21, which is 8 and 12 and 10 and 11, so we have all pairs:

`\begin{gathered} 4\colon(1+3) \\ 6\colon(2+4) \\ 13\colon(6+7) \\ 14\colon(5+9) \\ 20\colon(8+12) \\ 21\colon(10+11) \end{gathered}`