Question

How many gallons of a 30% alcohol solution and 90% alcohol solution must be mixed to get 12 gallons of a 50% alcohol solution

Answer 1

We must mix 4 gallons of a 90% alcohol solution and 8 gallons of a 30% alcohol solution.

We can solve the exercise writing two equations. In these equations let's call x the 30% alcohol solution and y the 90% alcohol solution:

- equation 1: x.(0.3) + y.(0.9) = 12.(0.5)

- equation 2: x+y=12

Now, we can replace x from the equation 2 on equation 1.

First, from equation 2 we resolve x=12-y so we can replace it on the equation 2:

`\begin{gathered} x.\mleft(0.3\mright)+y.\mleft(0.9\mright)=12.\mleft(0.5\mright) \\ (12-y)\cdot(0.3)+y\cdot(0.9)=12\cdot(0.5) \\ 3.6-y\cdot(0.3)+y\cdot(0.9)=6 \\ y\cdot(0.6)=6-3.6 \\ y=(2.4)/(0.6) \\ y=4 \end{gathered}`

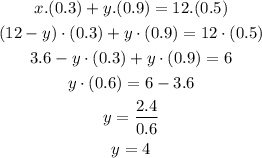
So, it is needed 4 gallons of 90% alcohol solution.

Finally, we replace the value of y=4 on the equation 2 to find x:

`\begin{gathered} x+y=12 \\ x+4=12 \\ x=12-4 \\ x=8 \end{gathered}`

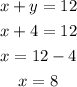
And It is needed 8 gallons of 30% alcohol solution.

We must mix 4 gallons of a 90% alcohol solution and 8 gallons of a 30% alcohol solution.