Question

Write the quadratic equation y=(x^2)-6x+7 in vertex form

Answer 1

`x^2-6x+7= \\ x^2-6x+9-9+7= \\ (x-3)^2-9+7= \\ (x-3)^2-2 \\ \\ \boxed{y=(x-3)^2-2}`

Answer 2

`\text{The vertex form is }y=(x-3)^2-2`

Explanation:

Given a quadratic equation
`y=x^2-6x+7`

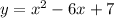
we have to write the equation in vertex form.

Comparing given equation with the standard equation
`y=ax^2+bx+c`, we get

a=1, b=-6 and c=7

`h=x_(vertex)=(-b)/(2a)=(6)/(2)=3`

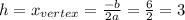
Substitute the value of x in given equation,

`k=y_(vertex)=1(3)^2-6(3)+7=9-18+7=-2`

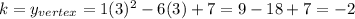
Now, put above values in vertex form of quadratic equation i.e

`y=a(x-h)^2+k`

`y=1(x-3)^2-2`

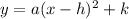
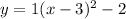
Hence, the vertex form is

`y=(x-3)^2-2`