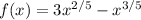
We get the derivative :
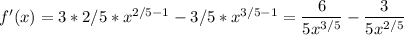
f'(x) is negative for x<0.
Let's look at the critical points other than at x=0:
f'(x)=0 <=> 6/5-(3/5)x^(1/5)=0 <=> x^(1/5)=(6/5)*(5/3)=2 hence x=2^5=32
There is a critical point at x=32; for x<=32 f' is positive, for x>=30 f' is negative.
The derivative is positive for positive xs and negative for negative xs, hence
f is increasing for 32>=x>0, and decreasing for x<0 and x>32