Answer:
Choice D.
Step-by-step explanation:
The vertex form of a parabola is given by
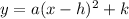
where (h, k) is the vertex.
Now, in our case we have the vertex at (2, 1); therefore, the above gives
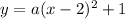
Now we just need to find the value of a.
We know that the parabola passes through the point (3, -2), meaning the equation must satisfy x= 3 when y = -2.
Putting in x = 3 and y = -2 in the above equation gives
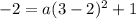
which simplifies to give
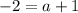
subtracting 1 from both sides gives
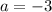
Hence, the equation of the quadratic function is
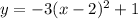
which is choice D.