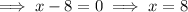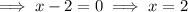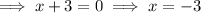Answer:

Explanation:
Given function:

Factor Theorem
If f(x) is a polynomial, and f(a) = 0, then (x – a) is a factor of f(x).
Therefore, since f(8) = 0, then (x - 8) is a factor of the function f(x):
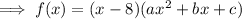
The coefficient of x³ is a.
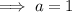
The constant 48 is equal to -8c.
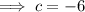
To find the value of b:
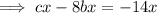
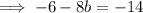
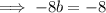

Therefore:
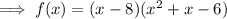
Factor (x² + x - 6):
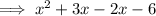
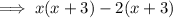

Therefore the fully factored function is:

To find the zeros of the function, set each factor to zero: