Question

someone someone please help it keeps cutting it off but it says determine which equation is parallel to line JK and which is perpendicular to line JK not all equations will be used so I have to put them in a perpendicular box and then the parallel box if somebody could help me

Answer 1

Given the information, we have that the line passes through the points (-5,5) and (-2,0), therefore, we can find the equation like this:

`\begin{gathered} \text{First we find the slope:} \\ m=(y_2-y_1)/(x_2-x_1)=(0-5)/(-2-(-5))=-(5)/(3) \\ m=(5)/(3) \\ \text{Now we use the point-slope formula (using the point (-2,0)):} \\ y-y_0=m(x-x_0) \\ \Rightarrow y-0=-(5)/(3)(x-(-2)) \\ \Rightarrow y=-(5)/(3)x-(10)/(3) \\ \text{Multiplying both sides by 3 we get:} \\ 3y=-5x-10 \\ \Rightarrow3y+5x=-10 \end{gathered}`

Now that we have the equation of the line, we can easily find the parallel and perpendicular. For the parallel, we need that the line use the same slope (m=-5/3), therefore, from the options, the equation 5x+3y=13 is the only parallel to the original line. Now, for the perpendicular we have:

`\begin{gathered} m_p=-(1)/(m)=-(1)/(-(5)/(3))=(3)/(5) \\ \text{ Using the same point as before (-2,0) we get:} \\ y-0=(3)/(5)(x+2) \\ \Rightarrow y=(3)/(5)x+(6)/(5) \\ \text{Multiplying both sides by 5 we get:} \\ 5y=3x+6 \\ \Rightarrow-3x+5y=6 \end{gathered}`

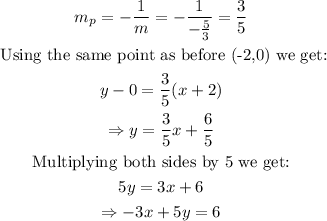
Therefore, the equation of the perpendicular line is -3x+5y=6