Given the information, we have that the line passes through the points (-5,5) and (-2,0), therefore, we can find the equation like this:

Now that we have the equation of the line, we can easily find the parallel and perpendicular. For the parallel, we need that the line use the same slope (m=-5/3), therefore, from the options, the equation 5x+3y=13 is the only parallel to the original line. Now, for the perpendicular we have:
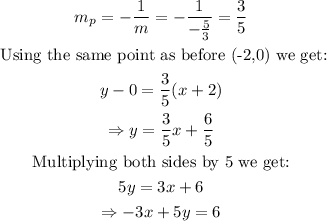
Therefore, the equation of the perpendicular line is -3x+5y=6