Question

Solve the equation. log, (-x) + log, (x - 10) = log, 24 Select one: O a. {-6 O b. O O c. {-6, -4) O d. {4,6

Answer 1

`\log (-x)+\log (x-10)=\log (24)`

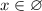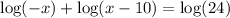
start by applying the log properties on the left side

`\log (-x^2+10x)=\log (24)`

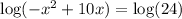
remember that when we talk about the logs they are defined for values greater than 0, determine the range in which will be defined

`\begin{gathered} -x^2+10x>0 \\ -x(x-10)<0 \\ x<0 \\ x-10<0 \\ x<10 \\ x=\mleft\lbrace0,10\mright\rbrace \end{gathered}`

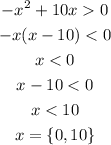
knowing that the values in order for the log to be true must be between 0 and 10, apply base 10 on both sides to cancel the log

`10^(log(-x^2+10x))=10^(\log (24))`
`\begin{gathered} -x^2+10x=24 \\ -x^2+10x-24=0 \\ \text{using the quadratic equation} \\ a=-1;b=10;c=-24 \\ x_1=4;x_2=6_{} \end{gathered}`

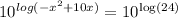
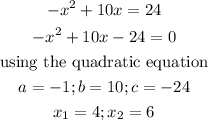
after having the values of the quadratic replace them on the equation

`\begin{gathered} x=4 \\ \log (-4)+\log (4-10)=\log (24) \\ \log (-4)+\log (-6)\\e\log (24) \end{gathered}`
`\begin{gathered} x=6 \\ \log (-6)+\log (6-10)=\log (24) \\ \log (-6)+\log (-4)\\e\log (24) \end{gathered}`

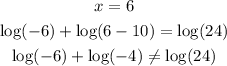
after seeing that with both solutions is false the statement, we can conclude that there are no solutions for x.

`x\in\varnothing`