Question

The equation x2 + y2 − 2x + 2y − 1 = 0 is the general form of the equation of a circle. What is the standard form of the equation?

Answer 1

x^2 + y^2 - 2x + 2y - 1 = 0

(x^2 - 2x) + (y^2 + 2y) - 1 = 0

(x^2 - 2x + 1) + (y^2 + 2y + 1) - 1 - 1 - 1 = 0

(x - 1)^2 + (y + 1)^2 - 3 = 0

(x - 1)^2 + (y + 1)^2 = 3

Answer 2

`(x-1)^2+ (y+1)^2=3`

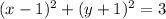
Explanation:

`x^2 + y^2 - 2x + 2y - 1 = 0`

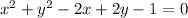
Standard form of the equation is
`(x-h)^2 + (y-k)^2= r^2`

To get standard form we apply completing the square method

`x^2-2x+ y^2+ 2y - 1 = 0`

Take coefficient of x and y . Divide it by 2 and then square it

`(2)/(2) =1` and 1^2=1

Add and subtract 1

`(x^2-2x)+(y^2+ 2y) - 1 = 0`

`(x^2-2x+1-1)+(y^2+ 2y+1-1) - 1 = 0`

`(x^2-2x+1)+(y^2+ 2y+1)-1-1- 1 = 0`

`(x^2-2x+1)+(y^2+ 2y+1)-3= 0`

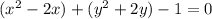
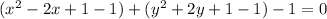
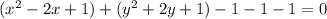
Now write the parenthesis in square form

`(x-1)(x-1)+ (y+1)(y+1)-3= 0`

`(x-1)^2+ (y+1)^2-3= 0` , add 3 on both sides

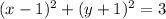`(x-1)^2+ (y+1)^2=3` is the standard form