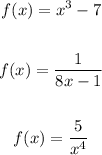Question

I don’t understand what the term one to one means

Answer 1

From the given functions, let's select the functions that are one-to-one functions.

A function is said to be a one-to-one function when it produces different outputs for different inputs (values of x).

The easiest way to determine if a function is a one-to-one function is to graph the function and use the horizontal line test.

Now, let's check the functions to determine.

• Function 1.

f(x) = x³ - 7

Since the leading exponent is an odd number, this function can be said to be a one-to-one function.

• Function 2.

f(x) = x² - 4

The leading exponent of this function is an even number. Since it is even, it will fail the horizontal line test. Therefore, the function is NOT a one-to-one function.

• Function 3.

`f(x)=(1)/(8x-1)`

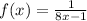
This function is a one-to-one function.

• Function 4.

`f(x)=(5)/(x^4)`

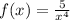
This function is a one-to-one function.

• Function 5.

f(x) = |x|

This function is NOT a one-to-one function since it will fail the horizontal line test.

Therefore, the functions that are one-to-one are:

`\begin{gathered} f(x)=x^3-7 \\ \\ f(x)=(1)/(8x-1) \\ \\ f(x)=(5)/(x^4) \end{gathered}`