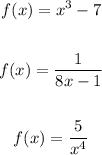From the given functions, let's select the functions that are one-to-one functions.
A function is said to be a one-to-one function when it produces different outputs for different inputs (values of x).
The easiest way to determine if a function is a one-to-one function is to graph the function and use the horizontal line test.
Now, let's check the functions to determine.
• Function 1.
f(x) = x³ - 7
Since the leading exponent is an odd number, this function can be said to be a one-to-one function.
• Function 2.
f(x) = x² - 4
The leading exponent of this function is an even number. Since it is even, it will fail the horizontal line test. Therefore, the function is NOT a one-to-one function.
• Function 3.
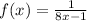
This function is a one-to-one function.
• Function 4.
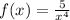
This function is a one-to-one function.
• Function 5.
f(x) = |x|
This function is NOT a one-to-one function since it will fail the horizontal line test.
Therefore, the functions that are one-to-one are: