Question

Find the area of the quadrilateral with the given coordinates A(-2, 4), B(2, 1),C(-1, -3), D(-5, 0).25 square units20 square units10 square units50 square units

Answer 1

Determine the length of side AB.

`\begin{gathered} AB=\sqrt[]{(-2-2)^2+(4-1)^2} \\ =\sqrt[]{16+9} \\ =5 \end{gathered}`

Determine the length of BC.

`\begin{gathered} BC=\sqrt[]{(-1-2)^2+(-3-1)^2} \\ =\sqrt[]{9+16} \\ =5 \end{gathered}`

Determine the length of CD.

`\begin{gathered} CD=\sqrt[]{(-5+1)^2+(0+3)^2} \\ =\sqrt[]{16+9} \\ =5 \end{gathered}`

Determine the length of side DA.

`\begin{gathered} DA=\sqrt[]{(-2+5)^2+(4-0)^2} \\ =\sqrt[]{9+16} \\ =5 \end{gathered}`

All sides of quadilateral are equal. So quadilateral is a square or rhombus with side of 5 units.

Determine the length of diagonal AC and BD.

`\begin{gathered} AC=\sqrt[]{(-1+2)^2+(-3-4)^2} \\ =\sqrt[]{1+49} \\ =\sqrt[]{50} \end{gathered}`
`\begin{gathered} BD=\sqrt[]{(-5-2)^2+(0-1)^2} \\ =\sqrt[]{49+1} \\ =\sqrt[]{50} \end{gathered}`

Diagonals are equal so quadilateral is a square.

Determine the area of square with side 5.

`\begin{gathered} A=5\cdot5 \\ =25 \end{gathered}`

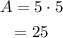
So area is 25 square units.