Question

Suppose that the scores on a statewide standardized test are normally distributed with a mean of 63 and a standard deviation of 2. Estimate the percentage of scores that were(a) between 59 and 67. %(b) above 69. %(c) below 59. %(d) between 57 and 67. %

Answer 1

Answer:

a) Percentage of scores that were between 59 and 67 = 95.45%

b) Percentage of scores above 69 = 0.135%

c) Percentage of scores below 59 = 2.2755%

d) Percentage of scores between 57 and 67 = 97.59%

Explanations:

The mean, μ = 63

Standard deviation, σ = 2

When x = 59

`\begin{gathered} z\text{ = }(x-\mu)/(\sigma) \\ z\text{ = }(59-63)/(2) \\ z\text{ = }-2 \end{gathered}`

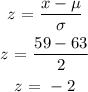
When x = 67

`\begin{gathered} z\text{ = }(x-\mu)/(\sigma) \\ z\text{ = }(67-63)/(2) \\ \text{z = 2} \end{gathered}`

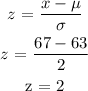
P(59 < x < 67) = P(-2 < x < 2) = 0.9545

Probability that scores fall between 59 and 67 = 0.9545

Percentage of scores that were between 59 and 67 = 95.45%

b) above 69

P(x > 69)

`\begin{gathered} z\text{ = }(x-\mu)/(\sigma) \\ z\text{ = }(69-63)/(2) \\ z\text{ = 3} \end{gathered}`

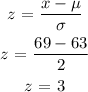
P(x > 69) = P(z > 3) = 0.0013499

Percentage of scores above 69 = 0.135%

c) below 59

P(x < 59)

`\begin{gathered} z\text{ = }(59-63)/(2) \\ z\text{ = -2} \end{gathered}`

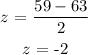
P(x < 59) = P(z < -2) = 0.02275

Percentage of scores below 59 = 2.2755%

d) between 57 and 67.

when x = 57

`\begin{gathered} z\text{ = }(57-63)/(2) \\ z\text{ = -3} \end{gathered}`

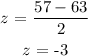
P(57 < x < 67) = P(-3 < x < 2) = 0.9759

Percentage of scores between 57 and 67 = 97.59%