Question

21. find the volume of the solid of revolution formed if the area enclosed between the curves y=x² and y=(x-2)² is rotated about the x-axis using integration

Answer 1

What you need to do is get hold of the area underneath the curve y=x² from x=1 to x=0. You then spin this area 360 degrees about the x-axis and double the result as there is symmetry between y=x² and y=(x-2)².

Use the formula:


`Volume=\int _( a )^( b ){ \pi { y }^( 2 ) } dx`

Ok, so let's solve the problem...


`V=2\int _( 0 )^( 1 ){ \pi { x }^( 4 ) } dx\\ \\ =2{ \left[ \frac { \pi { x }^( 4+1 ) }{ 4+1 } \right] }_( 0 )^( 1 )`


`\\ \\ =2{ \left[ \frac { \pi { x }^( 5 ) }{ 5 } \right] }_( 0 )^( 1 )\\ \\ =2\left\{ \left( \frac { \pi }{ 5 } \right) -\left( 0 \right) \right\} \\ \\ =\frac { 2 }{ 5 } \pi`

Answer:


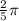
`\frac { 2 }{ 5 } \pi` units cubed.