Question

Physicists tell us that altitude h in feet of a projectile t seconds after firing is h=-16t^2+v0t+h0, where v0 is the initial velocity in feet per second and h0 is the altitude in feet from which it is fired. If a rocket is launched from a hilltop 2400 feet above the desert with an initial upward velocity of 400 feet per second, then when will it land on the desert ?

Answer 1

The formula that the physicists told was

`h(t)=-16t^2+v_0t+h_0`

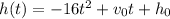
We know that

v₀ = 400 ft/s

h₀ = 2400 ft

Then let's put it into the formula

`\begin{gathered} h(t)=-16t^2+400t+2400 \\ \\ \end{gathered}`

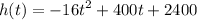
We want to know then it will land on the desert, in other words, when the height is equal to zero, then

`-16t^2+400t+2400=0`

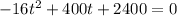
Then we must solve that quadratic equation, to solve it let's first divide all by 16

`\begin{gathered} -16t^2+400t+2400=0 \\ \\ -t^2+25t+150=0 \end{gathered}`

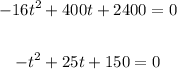
Because it's an easier equation to solve and the solution is the same. Now we can apply the quadratic formula

`t=(-b\pm√(b^2-4ac))/(2a)`

Plug the values

`\begin{gathered} t=(-25\pm√(25^2-4\cdot(-1)\cdot150))/(2\cdot(-1)) \\ \\ t=(-25\pm√(625+4\cdot150))/(-2) \\ \\ t=(25\pm√(625+600))/(2) \\ \\ t=(25\pm√(1225))/(2) \\ \\ t=(25\pm35)/(2) \\ \\ t=(25+35)/(2)=(60)/(2)=30\text{ seconds} \end{gathered}`

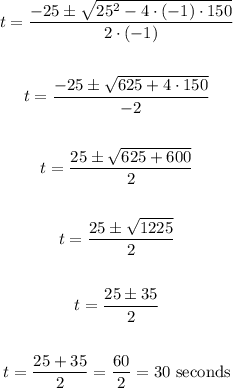
We can ignore the other solution because it's negative and negative time is not a valid solution. Therefore, 30 seconds after its launch, the rocket will land in the desert