Question

Write 0.611111111111 as a fraction PLEASE EXPLAIN STEP BY STEP!

Answer 1

We have to write N=0.6111... as a fraction.

This is a periodic number.

We start by transforming the number as:

`10\cdot N=10\cdot0.6111\ldots=6.111\ldots=6+0.111\ldots`

Now we take the periodic part we have (x=0.111...) and express it like this:

`10x=10\cdot0.111\ldots=1.111\ldots=1+0.111\ldots=1+x`

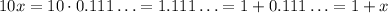
Then, we have:

`\begin{gathered} 10x=1+x \\ 10x-x=1 \\ 9x=1 \\ x=(1)/(9) \end{gathered}`

We use 10 to have the non-periodic part as an integer and the periodic part as a decimal.

Now we know that our periodic part of the number is equal to 1/9.

So we come back to N and complete:

`\begin{gathered} 10N=6+0.111\ldots=6+(1)/(9) \\ N=(1)/(10)(6+(1)/(9))=(1)/(10)((6\cdot9)/(9)+(1)/(9))=(1)/(10)\cdot(54+1)/(9)=(1)/(10)\cdot(55)/(9)=(55)/(90) \end{gathered}`

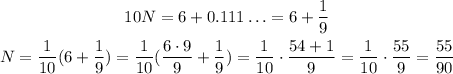
Then, 0.6111... as a fraction is 55/90.